Return to How to Use ROLL in Command Line
Interactive Mode for ROLL
This page shows how the user can play as a teacher to help the NBA (short for Nondeterministic Büchi Automata) learner based on the periodic FDFA learning to learn the language {a, b}* bω.
The user needs to use following command line to play with roll.
java -jar ROLL.jar play -periodic
To start the learning procedure, ROLL will ask you to initialize the alphabet of the target language. In this case, we set the alphabet to {a, b}. Note that for simplicity, we only use the letters from 'a' to 'z'.
Please input the number of letters ('a'-'z'):
2
Please input the 1th letter:
a
Please input the 2th letter:
b
At the beginning, the learner has to initialize and close the observation tables by asking you several membership queries.
Is w-word (ϵ, a) in the unknown languge: 1/0 0 Is w-word (ϵ, b) in the unknown languge: 1/0 1 Is w-word (ϵ, ba) in the unknown languge: 1/0 0 Is w-word (ϵ, bb) in the unknown languge: 1/0 1
When the learner constructs a conjectured NBA, it will ask an equivalence query for the following conjecture.
Resolving equivalence query for hypothesis (#Q=4)...
Is following automaton the unknown automaton: 1/0?
digraph {
0 [label="0", shape = circle];
0 -> 0 [label="b"];
0 -> 2 [label="b"];
0 -> 3 [label="b"];
0 -> 0 [label="a"];
0 -> 1 [label="a"];
1 [label="1", shape = circle];
1 -> 2 [label="b"];
1 -> 3 [label="b"];
1 -> 1 [label="a"];
2 [label="2", shape = circle];
2 -> 2 [label="b"];
2 -> 3 [label="b"];
2 -> 1 [label="a"];
3 [label="3", shape = doublecircle];
3 -> 2 [label="b"];
3 -> 1 [label="a"];
4 [label="", shape = plaintext];
4 -> 0 [label=""];
}
You can get the following graphical view of above dot text on the webpage Webgraphviz or by the xdot tool.
The above output automaton is clearly not the right conjecture. In this case, you can answer a counterexample, say b(ab)ω given by its decomposition (b, ab), which is accepted by the conjecture but is not in the target language, to the learner.
0 Now you have to input a counterexample for inequivalence. please input stem: b You input a stem: b please input loop: ab You input a loop: ab
The learner will ask several membership queries in order to analyze the received counterexample and to construct a new conjecture.
Is w-word (b, ab) in the unknown languge: 1/0 0 Is w-word (ϵ, ab) in the unknown languge: 1/0 0 Is w-word (ϵ, b) in the unknown languge: 1/0 1 Is w-word (ϵ, b) in the unknown languge: 1/0 1 Is w-word (ϵ, bb) in the unknown languge: 1/0 1 Is w-word (ϵ, ab) in the unknown languge: 1/0 0 Is w-word (ϵ, bab) in the unknown languge: 1/0 0 Is w-word (ϵ, bbb) in the unknown languge: 1/0 1 Is w-word (ϵ, aa) in the unknown languge: 1/0 0 Is w-word (ϵ, aab) in the unknown languge: 1/0 0 Is w-word (ϵ, ab) in the unknown languge: 1/0 0 Is w-word (ϵ, abb) in the unknown languge: 1/0 0
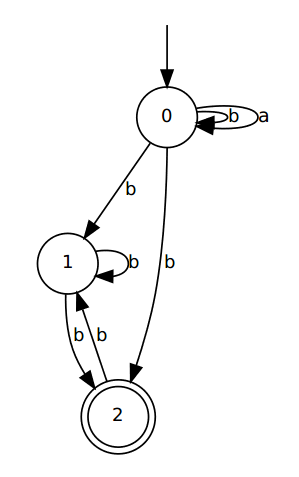
This time we receive the following conjectured NBA.
Resolving equivalence query for hypothesis (#Q=3)...
Is following automaton the unknown automaton: 1/0?
digraph {
0 [label="0", shape = circle];
0 -> 0 [label="b"];
0 -> 1 [label="b"];
0 -> 2 [label="b"];
0 -> 0 [label="a"];
1 [label="1", shape = circle];
1 -> 1 [label="b"];
1 -> 2 [label="b"];
2 [label="2", shape = doublecircle];
2 -> 1 [label="b"];
3 [label="", shape = plaintext];
3 -> 0 [label=""];
}
Above automaton is the right conjecture accepting the language {a,b}*bω. Thus we can reply with a positive answer to the learner, which means that the learner has completed the learning task.
1 Congratulations! Learning completed...
Following command allows the user to see more details about the learning procedure.
java -jar ROLL.jar play -periodic -v 2
Besides the output conjectures, ROLL also allows the user to see how the FDFA and its corresponding observation tables evolve during the learning procedure. Moreover, the log also shows the counterexample analysis information as described in paper [6].
The complete log information of an execution of above command is given as follows.
PLAYING,TABLE,PERIODIC,NONE,NBA,UNDER,verbose=2,bs=false,dot=false,inputfile=null,outputfile=null,outputA=null,outputB=null
2018/11/13 16:11:13 [ info] ROLL for interactive play...
Please input the number of letters ('a'-'z'):
2
Please input the 1th letter:
a
Please input the 2th letter:
b
Initializing learning...
Is w-word (ϵ, a) in the unknown languge: 1/0
0
Is w-word (ϵ, b) in the unknown languge: 1/0
1
Is w-word (ϵ, ba) in the unknown languge: 1/0
0
Is w-word (ϵ, bb) in the unknown languge: 1/0
1
Table/Tree is both closed and consistent
Leading Learner:
|| (ϵ, ϵ) |
=============
ϵ || - |
=============
a || - |
b || - |
Progress Learner for ϵ:
|| ϵ |
=========
ϵ || - |
b || + |
=========
a || - |
ba || - |
bb || + |
Resolving equivalence query for hypothesis (#Q=4)...
Is following automaton the unknown automaton: 1/0?
digraph {
0 [label="0", shape = circle];
0 -> 0 [label="b"];
0 -> 2 [label="b"];
0 -> 3 [label="b"];
0 -> 0 [label="a"];
0 -> 1 [label="a"];
1 [label="1", shape = circle];
1 -> 2 [label="b"];
1 -> 3 [label="b"];
1 -> 1 [label="a"];
2 [label="2", shape = circle];
2 -> 2 [label="b"];
2 -> 3 [label="b"];
2 -> 1 [label="a"];
3 [label="3", shape = doublecircle];
3 -> 2 [label="b"];
3 -> 1 [label="a"];
4 [label="", shape = plaintext];
4 -> 0 [label=""];
}
0
Now you have to input a counterexample for inequivalence.
please input stem:
b
You input a stem: b
please input loop:
ab
You input a loop: ab
Current FDFA:
//FFA-M:
digraph {
0 [label="0", shape = circle];
0 -> 0 [label="1"];
0 -> 0 [label="0"];
1 [label="", shape = plaintext];
1 -> 0 [label=""];
}
//FFA-P0:
digraph {
0 [label="0", shape = circle];
0 -> 1 [label="1"];
0 -> 0 [label="0"];
1 [label="1", shape = doublecircle];
1 -> 1 [label="1"];
1 -> 0 [label="0"];
2 [label="", shape = plaintext];
2 -> 0 [label=""];
}
Analyzing counterexample for FDFA learner...
Is w-word (b, ab) in the unknown languge: 1/0
0
DFA D_{u$v} for counterexample (u, v):
digraph Automaton {
rankdir = LR;
0 [shape=doublecircle,label=""];
0 -> 7 [label="a"]
1 [shape=circle,label=""];
1 -> 6 [label="a"]
2 [shape=circle,label=""];
2 -> 7 [label="a"]
3 [shape=circle,label=""];
initial [shape=plaintext,label=""];
initial -> 3
3 -> 4 [label="$"]
3 -> 5 [label="b"]
4 [shape=circle,label=""];
4 -> 1 [label="b"]
5 [shape=circle,label=""];
5 -> 2 [label="$"]
5 -> 3 [label="a"]
6 [shape=doublecircle,label=""];
6 -> 1 [label="b"]
7 [shape=circle,label=""];
7 -> 0 [label="b"]
}
Counterexample not in target: b$ab
final counterexample for the FDFA learner: b$ab
normalized factorization: (b, ab)
Is w-word (ϵ, ab) in the unknown languge: 1/0
0
Starting counterexample analysis in the learner (1,2) ...
Is w-word (ϵ, b) in the unknown languge: 1/0
1
Is w-word (ϵ, b) in the unknown languge: 1/0
1
Is w-word (ϵ, bb) in the unknown languge: 1/0
1
Is w-word (ϵ, ab) in the unknown languge: 1/0
0
Is w-word (ϵ, bab) in the unknown languge: 1/0
0
Is w-word (ϵ, bbb) in the unknown languge: 1/0
1
Is w-word (ϵ, aa) in the unknown languge: 1/0
0
Is w-word (ϵ, aab) in the unknown languge: 1/0
0
Is w-word (ϵ, ab) in the unknown languge: 1/0
0
Is w-word (ϵ, abb) in the unknown languge: 1/0
0
Finished counterexample analysis in the learner...
Table/Tree is both closed and consistent
Leading Learner:
|| (ϵ, ϵ) |
=============
ϵ || - |
=============
a || - |
b || - |
Progress Learner for ϵ:
|| ϵ | b |
=============
ϵ || - | + |
b || + | + |
a || - | - |
=============
ba || - | - |
bb || + | + |
aa || - | - |
ab || - | - |
Resolving equivalence query for hypothesis (#Q=3)...
Is following automaton the unknown automaton: 1/0?
digraph {
0 [label="0", shape = circle];
0 -> 0 [label="b"];
0 -> 1 [label="b"];
0 -> 2 [label="b"];
0 -> 0 [label="a"];
1 [label="1", shape = circle];
1 -> 1 [label="b"];
1 -> 2 [label="b"];
2 [label="2", shape = doublecircle];
2 -> 1 [label="b"];
3 [label="", shape = plaintext];
3 -> 0 [label=""];
}
1
Congratulations! Learning completed...