Table of Contents
EPMC - (An Extendible Probabilistic Model Checker, previously known as IscasMC)
Introduction
EPMC is a model checker for probabilistic models. It is a successor of the model checker IscasMC which only focuses on PLTL model checking over MDP. EPMC supports Markov chains and Markov decision Processes (MDP), and properties specified in PCTL, PLTL and their combination PCTL*. It implements the efficient algorithm in particularly tuned to handle linear time properties, see the report for details. EPMC is written in Java, while including a few off-the-shelf components like SPOT on the server side. The web interface on the client side is written in HTML and JavaScript, such that EPMC enjoys full portability: it can be run from any machine with internet access and a browser, be it a laptop or a mobile phone.
The main characteristics of EPMC are the high modularity of the tool, the possibility to extend EPMC with plugins to add new functionalities, and its availability on multiple platforms. EPMC achieves its flexibility by an infrastructure that consists of a minimal core part and multiple plugins that is very convenient to develop a new model checker based on the core parts of EPMC.
EPMC is mainly developed in Java, but accesses a few libraries written in C/C++ to increase performance or to access well established legacy code. Its graphical user interface (GUI) is a single static webpage. The GUI communicates with the backend, where core functions (like model checking) and high-privilege operations (like file I/O) are realised.
Models supported by EPMC
- Discrete Time Markov Chains (DTMCs)
- Markov Decision Processes (MDPs)
- Continuous Time Markov Chains (CTMCs)
- Stochastic Multi-player games (SMGs)
- Probabilistic Parity Games (PPGs)
(All input models can be specified in the PRISM format and JANI format.)
Properties supported by EPMC
- PCTL
- PLTL
- PCTL*
- CSL (in progress)
- Transient Properties (in progress)
- Expected Rewards (in progress)
We give some example LTL properties which can be specified in EPMC. In our tool, such formulas can be used in form P=?[…] for Markov chains and as Pmax=?[…] or Pmin=?[…] for Markov decision processes, where … denotes the one of the following formula under consideration:
- Bounded responsibility property,
(G req1 ⇒ F<=bound reply1)& … & (G reqn ⇒ F<=bound replyn): for a family of components, each componentireplies to a given request within a given time bound. - Bounded responsibility property with fairness,
(GF req1 & … & GF reqn) & (G req1 ⇒ F<=bound reply1) & … & (G reqn ⇒ F<=bound replyn): similar to bounded responsibility, suitable forPmax=?in MDPs. The fairness ensures that the system is scheduled such that the request occurs infinitely often. - Bounded responsibility property with fairness,
(GF req1 & … & GF reqn) ⇒ ((G req1 ⇒ F<=bound reply1) & … & (G reqn ⇒ F<=bound replyn)): similar to bounded responsibility, suitable forPmin=?in MDPs. The fairness ensures that the system is scheduled such that the request occurs infinitely often.
Manual, structure of the EPMC
EPMC has three main components: the frontend web interface, the backend for handling requests from the frontend, and the model checker engine. A database engine is used to store information.
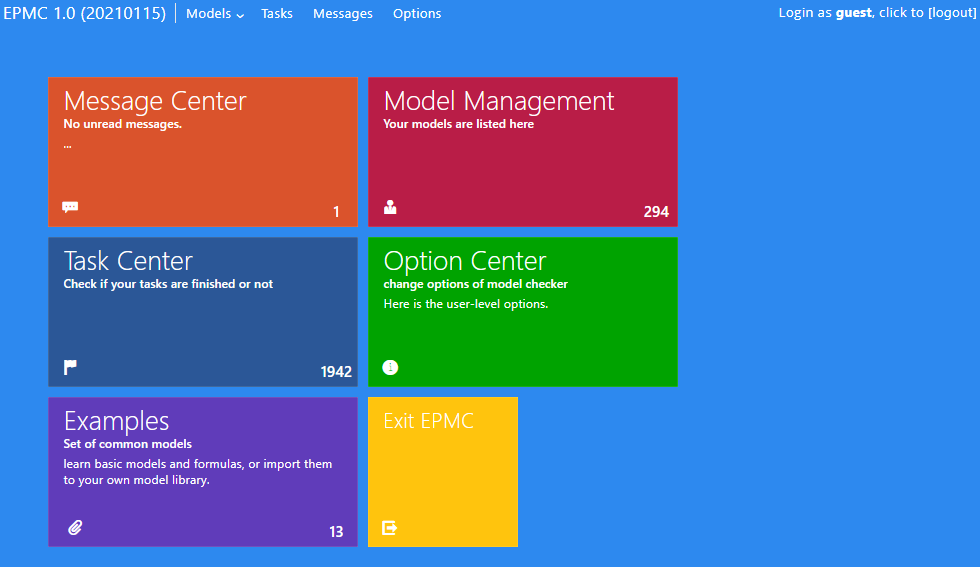
The Frontend Web Interface: The frontend allows for logging into the system, either as a guest or as a registered user. Guest users can experiment with most of the features of the tool, but they have limited resources, for instance small timeout values.
After logging into the system, it offers several views, including:
- Message Centre. The message centre provides the user recent news. Particularly, one can post messages, send models to other users as well as receive models shared by other users.
- Model Centre. The model management centre lists available models, their type (currently only PRISM models are supported), comments, options, last updated snapshot and all available operations for the model. From the menu above one can also upload or create new models. The properties are associated to models. For each model, one can create and analyse these properties. Currently, EPMC supports Markov chains and MDPs and properties in PCTL*. Once one clicks on one of the models in the list, one enters the editing page. In the editing page, models can be edited, and properties can be added, modified, or removed. A model may have more than one associated property.
- Task Centre. In the model centre, the user can choose to check selected properties or all properties. This is referred to as a task. Note that a task is created as a snapshot of the current model, (selected) properties and options. This allows the user to modify the model/properties and submit several tasks without having to wait for the termination of the previous submitted tasks. The task, together with the corresponding options, will be sent to the server side to be handled. In the task centre, one can find a list of all submitted tasks from the user. For each task, one can track the current status, find the final results once available, see the complete log generated by the model checker, or remove the task.
- Option Centre. From the option centre the user can set the user level options. Moreover, for each model to be analysed, one may modify certain options and get model level options. The model level options have higher priority and will overwrite user level options.
- Example Centre. From the example centre, the user can directly import several examples together with associated properties into her own account.
The Interface. While the frontend does not play a role in the evaluation of the model, it includes a fast syntax check that allows for checking the syntactical correctness of the model while interacting with the editor.
The part available to the frontend is a stand-alone program (on the server side) that makes use of only a small part of the classes in the model checker engine. This lightweight version is only used for checking the syntactical correctness of models from the client side, while the full version on the model checker site also constructs the respective models and automata. These syntactical correctness checks are simple and can thus be done efficiently on-demand, bypassing the scheduling queue.
The Database, powered by MySQL™, contains all information needed to elaborate the models: besides the user details, it stores the models and the relative properties defined by the user, as well as the tasks the user creates by requiring an operation on the model. Each task is created by the frontend DBMS module as snapshot of the model and the corresponding properties and options, such that it is not affected by subsequent changes. Once a task is completed, it is updated by the backend DBMS module with the evaluation of the properties (or with an error message), according to the model checker outcome. The tasks are kept until the user explicitly removes them via the task centre.
The Backend. The main job of the backend is to poll tasks from the database and evaluate them. It currently adopts a FIFO approach to retrieve the tasks from the DBMS module. These tasks are then sent to several instances of EPMC that run in parallel in independent worker threads. Once a worker completes her task, she sends the outcome to the data store, whose main jobs are to keep track of busy workers and to collect the results. Since the evaluation of a task may take some time, the worker periodically sends status updates to the data store. The result collector retrieves the available results from the data store and forwards them to the database via the backend DBMS module.
The Model Checker Engine. The model checker is the working horse of the system. Each work thread will parse and translate the model and the specification it is going to be checked against. For complex LTL subformulas (that is, for each linear part φ of PCTL* outside of the simple PCTL operators), we first use SPOT to generate the generalised Büchi automaton. Unless this is already deterministic, we then use our layered approach, which uses first subset constructions (with an over- and underapproximation of the acceptance condition), and subsequently refines them (where necessary) first to a breakpoint construction (again with an over- and underapproximation of the acceptance condition) and then to the deterministic Rabin automata. The product of the automaton and model is an MDP equipped with accepting conditions. These accepting conditions are used to identify accepting states in the product, after which the problem reduces to a probabilistic reachability problem for MDPs. The reachability problem is a central problem in probabilistic model checking, and is well studied. One can apply value iteration or policy iteration to solve it. Currently, EPMC uses a value iteration approach based on Gauss-Seidel or Jacobi method. After the evaluation, it returns the results to the backend.
Access to EPMC
- Download: EPMC is now available publicly. It can be obtained on GitHub, at this repository.
Please follow our wiki documentations to build and use EPMC. - Online version of EPMC is available here. Screenshot of EPMC online:
EPMC Plugins
Plugin: EPMC-PETL
Introduction
This tool is for model checking probabilistic multiagent systems with respect to the probabilistic epistemic logic PETL, which can specify both temporal and epistemic properties. We consider memoryless uniform schedulers in this problem, and the basic idea is to reduce the model checking problem into a mixed integer non-linear programming problem, which can then be solved by using an SMT solver. For more information, please check https://www.ijcai.org/proceedings/2018/661.
How to install and use
This tool is implemented as a plugin in ePMC. The source code can be found at https://github.com/fuchen1991/epmc-petl. All the implementation details related to PETL model checking are under “epmc-petl/plugins/propertysolver-petl”. And you can find the experiment files used in the paper under “experiment_files”. For building, running and other information about EPMC, please visit https://github.com/ISCAS-PMC/ePMC.
To perform PETL model checking, please set the following options:
--property-solver propositional-explicit,operator-explicit,pctl-explicit-next,petl-explicit-knowledge,pctl-explicit-until-uniform
--prism-flatten false
--model-input-type mas
--property-input-type petl
--smtlib-command-line z3 -smt2 {0}
--smtlib-version v25
--constraintsolver-solver smt-lib
--model-input-files /path/to/your-model /path/to/your-equivalence-relation
--property-input-files /path/to/your-property
You need to prepare 3 files: one for the model, one for equivalence relations, and one for properties.
The models should be in the PRISM format. Note that we redefine the composition of the modules to make the agents all take one local action in each transition, so the transitions from different modules will not synchronize according to the parallel composition operator.
The equivalence relations are described in this format:
equiv agent1 -- formula1; -- formula2; ...... equiv end equiv agent2 -- formula1; -- formula2; ...... equiv end ...... ......
Each agent in the model has a “equiv (agent name) … equiv end” block, and each block contains a set of formulas. You can use the variables used in the model. All the states satisfying the same formula are regarded as equivalent by the agent. So you can not write formulas such that one state satisfies two or more formulas. If one state can not satisfy any formula, it’s not equivalent to any other states.
The knowledge properties are described like this:
K {agent} (state_formula)
E/C/D {agent1,..., agentn} (state_formula)
Other properties can be described by the PRISM language.
Plugin: dpCTL
Introduction
Differential privacy is a framework for designing and analyzing privacy measures, which has become a gold standard in data privacy. In this tool, the branching time temporal logic dpCTL is developed for specifying differential privacy. Several differentially private mechanisms are formalized as Markov chains or Markov decision processes. Using formal models, subtle privacy conditions are specified by dpCTL. In order to verify privacy properties automatically, model checking problems are investigated. We implement a model checking algorithm for Markov chains and for MDPs, it's shown to be undecidable.
Our tool is built as a plugin of the model checker EPMC, and now is publicly available on GitHub at this repository. It now supports input files consisting of models and properties (both in the standard prism format.) For more information on how to use the tool, please refer to this page How to use the tool.
Case Studies
We have successfully analysed several case studies. Most of them are taken from the PRISM webpage (our tool supports the PRISM language directly)
- Workstation cluster: The model describes two clusters of workstations, connected by a backbone. Workstations and other components might fail with a certain rate but can be repaired afterwards. We considered properties about the order of component failures.
- Randomised Self-Stabilising Algorithms (Israeli and Jalfon): This self-stabilising protocol is a ring-shaped network. There, several tokens might exist, the protocol tries to reduce the total number to one. We considered a property about the order of the number of tokens existing.
- Randomised mutual exclusion: In this mutual exclusion protocol, we successfully analysed a number of properties from [ChatterjeeGK13].
- Gossip Protocol: Gossip protocols are used to quickly spread updates to information over a network, resembling the way actual gossip works. For the version we considered, we successfully analysed a property based on a pattern formula of [DwyerAC98]..
- Randomised Dining Philosophers: In this probabilistic version of the dining philosophers problem, we analysed a property obtained by instantiating a pattern from [DwyerAC98]..
- Firewire: The Firewire protocol is used for high-speed data transfer. The property we analysed was derived from [DwyerAC98].
Other projects
The following are projects related to EPMC:
- EPMC-PAMC: A model checker for probabilistic alternating-time Mu-Calculus.
- dpCTL: A model checker for differentially privacy verification.
- ROLL: A learning based tool for models inferring.